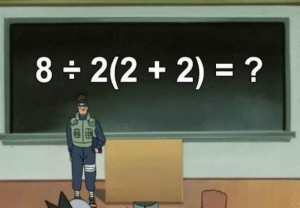Поводом для написания данной статьи стала недавняя публикация одним популярным буржуазным интернет-ресурсом — группой NecroTV в ВК (немногим менее 200 тыс. подписчиков) небольшого теста. Аудитории ресурса предлагалось решить математический пример из начальной школы:
8:2(2+2)=?
Вариантов ответа два:
(1) 16
(2) 1
В опросе приняло участие более 8,6 тыс. посетителей ресурса, из них около 53% выбрали первый (правильный) ответ, остальные – второй. Никаких комментариев по данному тесту администрация ресурса не дала.
Мотивация по публикации данного теста-опроса NecroTV не афишировалась; подборка постов там внешне совершенно бессистемная (то бессловесный набор омерзительных или шокирующих фотографий, то рисунок какого-нибудь абстракциониста и по совместительству заядлого курильщика опиума, то видео какого-то яркого события, например, митинга в Москве), администрация ресурса не утруждает себя объяснениями своей аудитории, по какому принципу она формирует повестку дня, посты там обычно не сопровождаются никакими комментариями администрации.
Не модерируются, по-видимому, и комментарии посетителей ресурса: мещанская аудитория предоставлена сама себе, и под постами количество комментариев порой доходит до многих сотен; посетители группы частенько не сдерживают себя барьерами приличий, с лёгкостью опускаясь до площадного мата даже по совершенно безобидным поводам. Читать все комментарии – нечеловеческая задача. В день размещается десять-двадцать постов, так что подача материала напоминает калейдоскоп, и отыскать заинтересовавший пост даже недельной давности не так-то просто: информация просто тонет под валом вновь поступающей. В общем, обыкновенная интернет-помойка.
И тем не менее публикация подобных задачек – не редкость в российском, да и в зарубежном интернет-пространстве, поэтому мы всё-таки остановимся на данной публикации как на типовой для буржуазной медиасреды. Тем более, что результат теста на первый взгляд шокирующий: почти половина респондентов не справилась с тестом. Возникло два вопроса: 1. В чём дело, почему такой разброс в ответах? 2. Зачем данный буржуазный ресурс разместил этот тест, и, в более общей форме: зачем вообще размещаются подобные тесты?
Признаться, первое, что приходит на ум, — это то, что пример из строго математического превращён в пример на внимательность: для этого достаточно из выражения убрать знак умножения, и рассеянные или думающие о чем-нибудь более важном люди будут попадаться «на удочку», автоматически выполняя деление последним действием. Ещё один «крючок», довольно распространённый, — это когда задают задачу заведомо ниже уровня подготовки человека, предподнося её как испытание. Не очень внимательный, неуверенный или отвлечённый чем-то человек будет чувствовать подвох «на ровном месте» и может совершить ошибку, которую никогда бы в жизни не допустил в обстановке, когда задача поставлена с уважением к его достоинству и без педалирования его неуверенности. Однако результат теста, когда мнения разделились практически «50 на 50», заставляет задуматься, что проблема глубже, чем кажется на первый взгляд.
Для полного понимания проблемы пришлось прочитать комментарии тех, кто ответил неправильно. Эти люди апеллировали к… Википедии — конкретно, к англоязычной страничке «Order of operations» («Приоритет операций»). Помимо этого, апеллируют к калькуляторам, которые при вводе данного выражения (с пропущенным знаком умножения) выдают на выходе значение 1, а также к некоторым современным российским учебникам, как попка-попугай, повторяющим любые глупости англоязычных «законодателей мод».
Действительно, Википедия, а следом и ряд современных учебных пособий педалируют двусмысленность порядка совершения математических действий! При этом «умники» ссылаются на американский журнал «Physical Review» («Обзор Физики»), где в инструкции по приёму рукописей операция умножения имеет приоритет перед делением, если последнее обозначается косой чертой. Помимо этого, Википедия ссылается на Ландау и Лифшица, которые в третьем издании Курса Теоретической Физики в разделе «Механика» на стр. 22 допускали выражения, как, например, hPz/2π (авторы имели в виду деление на произведение 2π), а также на первый том Феймановских лекций по физике, где тоже имеют место подобные злоупотребления.
Допустим, что контекст выражений в томах Ландау с Лившицем и Феймана не оставляет никакой двусмысленности в их интерпретации. Допустим также, что конвенция написания формул в конкретном журнале по физике хорошо известна читающим его, заранее оговорена и не вызывает у них никаких недоумений.
Однако это неправда: подобная фривольность в написании считается в научном мире дурным тоном, неуважением к читателю, выраженном в понуждении последнего напрягать внимание и вчитываться в детали, которые на самом деле отвлекают от концентрации на действительно существенном и сложном. Прогрессивные учёные всего мира борются с подобными явлениями.
Но у буржуазии иная повестка дня. И то, что считается дурным тоном, обернулось прецедентом, за который не замедлили ухватиться буржуазные деятели в области науки и образования. Они – учредители правил в этих областях, и решения по таким вещам, как установление жёстко стандартизированных во всей технической литературе, включая и образовательную, толкований приоритета операций принимаются не на научных конференциях. Оно принимается выше, во всевозможных комиссиях, в которых заседают давно порвавшие с наукой, предавшие науку либо вообще не имеющие к науке отношения люди. Отбор в эти комиссии проходит по принципу верности господствующему классу, не заинтересованному в просвещении масс. И решение это негативное: поощряется дестандартизация интерпретации приоритета.
Вдумайтесь только: обсуждение и упоминание двоякости толкования приоритета действий, совершенно нелепого с точки зрения математики, где двоякость просто исключена по определению, проникли на страницы школьных пособий! Вот, пожалуйста, полюбуйтесь:
Дальше больше. Буржуазные холуи от образования на полном серьёзе пытаются навязать школьникам некую несовместимость алгебры и арифметики. Полюбуйтесь:
Как результат, людям навязывают нелепые идеи, что приоритеты действий, принятые в арифметике, основным понятием и объектом которой являются числа, отличаются от приоритета тех же действий с числами, но только в алгебре.
Но это абсурд: арифметика и есть элементарная алгебра чисел. Просто алгебра имеет дело не только с числами, но и с объектами иной природы, например, с матрицами, с операторами и т.д. Да и числа в алгебре могут рассматриваться с более абстрактной точки зрения, но не суть. Никаких исключений нет, как нет никакого приоритета умножения над делением! Природа у деления и умножения в алгебре одна и та же: деление на ненулевое число x эквивалентно умножению на число 1/x. И наоборот, умножение на ненулевое число х эквивалентно делению на число 1/x.
На этом процесс дестандартизации приоритета операций не заканчивается. В подрывной деятельности на этом поприще не отстают и создатели программного обеспечения. Например, во всем известной и широко распространённой программе Microsoft Excel так называемая унитарная операция умножения на минус единицу имеет приоритет над бинарными, в том числе и над возведением в степень, т.е. умножение имеет приоритет над возведением в степень. Абсурд! Хотите – проверьте сами, почти у каждого есть эта программа на компьютере. Если вы вобьёте в клеточку окна Excel выражение =-3^2 и нажмёте на ввод, то получите 9. Таким образом, получается, что −32 =(−3)2 = 9. Хотя правильный ответ будет -9.
В реальности ничто не мешало создателям данной программы ликвидировать эту двоякость толкования. Однако поленились. Теперь пользователю, чтобы получить -9, приходится либо использовать скобки =-(3^2), либо отказываться от унитарной операции и вводить =0-3^2, либо явно умножать на минус единицу =-1*3^2. Невнимательный человек запросто может ошибиться.
Ловят рассеянных людей и, как мы упомянули выше, создатели калькуляторов. Это продемонстрировано на фото.
Это уже самое настоящее издевательство над математикой. И над трудящимися. Над нашими детьми, которые учатся по дестандартизированным правилам, дебилизирующим любую самую простенькую проблему. Программистам ничто не стоит обойти эту двоякость. Но кто заказывает программный продукт? А заказывает его жалкая кучка подонков, владеющих средствами производства этих калькуляторов, через своих верных холуёв-менеджеров, которые держат «нос по ветру», зная, как наиболее эффективно угодить своим хозяевам.
Да-да, продукт создаётся не для удовлетворения потребности трудящегося населения, а для удовлетворения запроса буржуазии. И этот запрос не ограничивается извлечением прибыли. Этого уже недостаточно. Прибыль, как и право собственности на средства производства, ещё нужно удержать. И одним физическим насилием здесь не обойтись: оно слишком грубо — терпение трудящихся может очень быстро лопнуть, и тогда держись! В ответ на физическое насилие получишь тоже физическое насилие, а насилию миллионов и миллиардов противостоять невозможно. Буржуазия прекрасно это знает, и для удержания в узде трудящихся, в первую очередь рабочего класса, она прибегает к иному насилию — идеологическому. Проще говоря, к дезориентации и деморализации своего непримиримого классового врага. И здесь буржуазная система «образования» играет ключевую роль. Эта роль заключается в имитации просвещения и насаждении невежества, в том числе и с помощью дестандартизации того, что кровь из носу обязано быть стандартизированным.
Вот так, на простом примере мы пронаблюдали общемировое наступление буржуазии на трудящихся, вскрыли важнейший элемент ее классовой борьбы. Подобное наступление ведётся классом буржуазии (действительно умирающим, раз ему стал опасен даже элементарный уровень образованности трудящихся!) по всем фронтам, не только в математике, но и в биологии, химии, физике, и особенно, разумеется, в общественных науках.
***
Попробуйте теперь сказать людям, выбравшим в тесте второй ответ, что они ответили неправильно!
В общем, ничего удивительного теперь в результате опроса нет. При такой дестандартизации интерпретации порядка арифметических действий опрос получился… нематематический. Это откровенное издевальство над аудиторией. Не составляет никаких сомнений, что разместившие данный пост с тестом прекрасно знали о двоякости. И умолчали. Ни до, ни после теста они никак не прокомментировали эту действительно серьёзную проблему.
Так какую цель преследовал данный тест? Оценить культурный уровень аудитории?
Нет. Создать его! Вернее, опустить ниже плинтуса. На ровном месте максимально сбить с толку аудиторию, и без того запутавшуюся и не понимающую что к чему. Заставить своих читателей материть друг друга, максимально разобщить их, закрепить и углубить ту самую неуверенность их в своих знаниях. А значит, цели публикации данного теста совпадают с целями разрушителей образовательных стандартов.
И по такому же принципу работают все буржуазные социальные опросы и тесты. Они не оценивают общественное мнение и культурный уровень, не анализируют их, а создают! Под предлогом выяснения отношения к определённому событию или проблеме в общественное сознание вносится яд буржуазной идеологии, задаётся повестка дня, выгодная буржуазии, а не трудящимся, углубляется невежество, закрепляются нужные буржуазии поведенческие стереотипы и многое другое.
***
Как и любой другой информационный ресурс, МЛРД «Рабочий путь» тоже создаёт общественное мнение, тоже влияет на культурный уровень. Но, в отличие от буржуазных пропагандистских площадок, мы не скрываем этого. Потому что мнения и уровни у нас отличные от тех, которые задают буржуазные ресурсы. Диаметрально противоположные! Буржуазии для сохранения своего господства нужна ложь, а нам, отражающим классовые интересы рабочего класса, требуется только правда, чтобы лишить буржуазию этого господства.
Возвращаясь к теме предложения аудитории ресурса решить какую-нибудь математическую задачу, невольно вспоминается положительный опыт советского социализма. В советских газетах и журналах читателям частенько предлагалось решить не задачки из программы начальной школы, а олимпиадные задачи по математике, серьёзные и красивые шахматные задачи, инженерные задачи на сообразительность и изобретательность. Это была действительная забота о высоком культурном уровне трудящихся. Решением этих задач можно было по праву гордиться, такими задачами можно было поделиться с друзьями, коллегами, увлечь своих детей.
К сожалению, с победой контрреволюции в Советском Союзе приходили в упадок и развивающие рубрики с задачами; олимпиадные задачи и интересные головоломки вытеснялись бессмысленными кроссвордами и ребусами, сборники занимательных и развивающих задач сменялись подборками анекдотов и афоризмов и т.д. Однако эта важная тема выходит за рамки данной статьи.
Идея вести рубрику с шахматными и олимпиадными задачами приходила в голову и редакции РП. Конечно, идеальным местом ведения такой рубрики была бы пролетарская периодика, где регулярно публиковались бы интересные и развивающие задачи и ответы на задачи, размещённые ранее. Надеемся, что создание такой периодики – дело ближайшего будущего.
А пока можем в качестве пробного шага предложить нашим читателям небольшую нестандартную математическую задачу для 7-го класса (советской десятилетки). И хотя она даже близко не доходит по сложности до уровня задач, размещаемых в советских журналах 1940-60-х гг., — до него ещё расти и расти, — над ней тоже не зазорно даже технически подготовленному человеку поломать голову самому, её тоже не стыдно будет предложить своим друзьям и детям.
Итак, задача:
Дано трёхсотзначное число, в котором сто цифр — нули, сто — единицы, сто — двойки. Может ли оно быть полным квадратом?
Попробуйте свои силы, товарищи. Решение мы опубликуем в продолжении данной статьи, в котором мы планируем, помимо всего, ответить на некоторые довольно распространённые, увы, сомнения по поводу полезности умения решать математические задачи.
О.Зотов, д.м.н., 11.08.2019г.
По калькуляторам. Действительно, такая проблема есть, и она ПОЛНОСТЬЮ решена в калькуляторах с обратной польской записью, например советском МК-61.
Сделаю замечание по excel. Если в excel ввести =8/2*(2+2), то и получим правильный ответ, то есть 16. Проблема скобок действительно имеет место, она серьезно затрудняет ввод сложных математических выражений, но вызвана она как раз строгостью выполнения порядка математических операций в excel при не очень удобном способе ввода.
Например, рассмотрим формулу f=1/2π*R*C. Если верить дебильному учебнику, приведенному автором, записана ВЕРНО. На самом же деле, эта запись соответствует R*C/2π. И именно так ее воспримет excel или matlab. Правильная запись для excel =1/(2*ПИ()*R*C), что и соответствует верной записи по правилам.
Но вот с excel автора я поправлю. Почему?
Во-первых, есть ошибка или опечатка:
«Теперь пользователю, чтобы получить -9, приходится либо использовать скобки =-(3)^2»
Если сделать так, ответ будет все равно 9! Верно =-(3^2). Возможно, это опечатка. Ее следует исправить.
Во-вторых, в excel, ПРЯМО написано в руководстве, что операция возведения в степень имеет приоритет на остальными, за исключением операций ссылки на ячейку, «процента» и СМЕНЫ ЗНАКА. Последним, строго говоря не есть математические операции (за исключением «процента»). Смысл этой операции в сокращении и удобстве:
=9%*3 результатом будет иметь 0,27, что эквивалентно записи 0,09*3. При этом
=9%*3^2 даст 0,81 что эквивалентно 0,09*3^2
Запись =-3^2 НЕ ЭКВИВАЛЕНТНА -1*3^2. Аналогом операции (-) является кнопка /-/ на калькуляторе МК-61 или операция (0-х). Сделано это как раз для того случая, когда вместо константы в выражении будет ссылка на ячейку, которая может содержать и отрицателен число.
Спасибо за интересную задачу.
Спасибо за указание на опечатку. Сейчас исправлю.
Совершенно верно. Запись -3 трактуется как константа -3, и парсер выделяет -3 ^ 2 как выражение.
1 переменная = -3
2 переменная = 2
Само выражение как лексему операции возведения в степень.
Математика — точная наука, от интересов правящего класса не зависящая.
Ошибаетесь! Математика не просто зависит от интересов правящего класса. Она их обслуживает.
Нет. Интересы правящего класса обслуживают СМИ, «статистические» и «научные» институты, призванные укреплять власть в стране (точнее — сглаживать возрастающие противоречия в капиталистическом обществе).
Математику они используют как инструмент. А мухлюют в основном со статистикой, методикой «подсчетов» и прочим.
Есть разница )
Что ж, ваши заблуждения ещё раз демонстрируют необходимость регулярно возвращаться к теме партийности науки.
В математике, как и в формальной логике математические правила и правила правильного мышления общие для всех классов. По крайней мере должны быть такими. Вопрос только как правящий класс использует математику, искажая правила вычислений.
В статье пишется именно об этих искажениях буржуями общепринятых математических правил, и о причинах и последствиях этих искажений. А раз они вмешались в математику, искажая правила, то значит они ее присвоили себе, т.е. математика стала служить им. Вот и классовость наук.
Даже в формальной логике проявляется партийность науки, у Строговича тому немало примеров (https://sheba.spb.ru/vuz/logika-1949.htm)
Совершенно верно! Об этом будет немного рассказано во второй части статьи.
получается приложение к диалектическому материализму не верно? потому как там объясняется, что формальная логика грамматика и арифметика есть элементарные науки и без логики ты не можешь мыслить как без грамматики не можешь грамотно писать.
И как это у человека получается умножить -3 само на себя и получить отрицательное число?
Читайте вторую часть статьи.
Поистине мозгодробительная задача. Невольно осознаешь, что стал жертвой профессиональной деформации — последствия современной жизни. Когда работа сводится к рутинным решениям однотипных задач. Многое забывается, даже основы математики. Это печально.
Подсказка для читателей: рассмотрите понятие «цифровой корень числа» и его свойства.
вот это да! Столько математики было в ВУЗе, а до вашей подсказки никогда о понятии «цифровой корень числа» не слышал! Образование получал называется…
Мдааа… математика — царица наук! «Факт!»)
Как ВИЛ сказал: если бы аксиомы математики противоречили чьим-то интересам, то их бы опровергали…
Хороший пример партийности математки в статье, спасибо.
>> −3в_степени_2 =(−3)2 = 9. Хотя правильный ответ будет -9. — какая будет обратная функция?
А при чём здесь обратная функция? Обратная к чему? Здесь прямая функция трактуется создателями программы по-идиотски. Причём эта трактовка не спровоцирована нерешаемостью (или значительным усложнением решения) проблемы создания алгоритма, при котором приоритет действий будет привычный для пользователя и математически правильный.
Не на то внимание обращаете. Статья не о программе Excel.
Я не об «Экселе». В встроенном калькуляторе винды нет разницы между -3^2 и (-3)^2, в другом, «Microsoft Mathematic», есть такая разница.
Про обратную функцию спросил, чтобы понять, как из -9 получить -3 извлечением квадратного корня. Без мнимой единицы не обойтись.
Не помню ни из школьной, ни из институтской программы ваше правило, что -3^2≠(-3)˄2. Кстати, следует ли тогда, что -3≠(-3)?
Оставьте в покое комплексные числа, они здесь не при чём. У функции f(x)=-x^2, хоть она и определена и непрерывна для всех вещественных значений аргумента, не существует обратной на всей вещественной оси, потому что функция в общем немонотонная: разным значениям аргумента может соответствовать одно и то же значение функции. Поэтому говорить о функции, обратной данной, можно только на участках монотонности, например, только для всех неположительных х. Но мне бы не хотелось здесь расписывать все детали — всё-таки у вас институт за плечами, освежите понятие обратной функции самостоятельно. Советские школьные учебники по «Алгебре и началам анализа» доступны.
Правило, что -3^2≠(-3)˄2 не моё, а математическое: слева сначала выполняется более приоритетное возведение в степень, потом умножение результата возведения в степень на минус единицу. Справа число -3 возводится в квадрат. Слева получается -9, справа получается 9.
Тому, что одному и тому же выражению присваиваются в разных калькуляторах разные значения, посвящена солидная часть статьи, под которой мы комментируем!
И кстати, это только первая часть статьи. Давайте дождёмся публикации продолжения.
Какие именно советские учебники Вы бы посоветовали. Каких авторов и каких лет?
Заранее спасибо, товарищ. Я учился в советской школе, но восемь лет, а в техникуме нам эту тему слишком быстро и скомкано подавали. Если вообще было дело.
Заранее спасибо, товарищ!
Возможно, об этом будет сказано во второй части статьи. Она выйдет на днях. Если нет, то тогда вернёмся к этому моменту отдельно.
Спасибо, подожду, товарищ)
Вторая часть и так получилась большой, и автор решил не загромождать её дополнительной информацией. Значит, к вашему вопросу вернёмся отдельно.